中学の時からずっと腑に落ちなかった系統の問題が今解りました。
なんか嬉しいから記念に＆忘れないように書いとく。今後似た問題に生徒が詰まったらめっちゃ教えちゃろう(笑)
とりあえず使うのは
中点連結定理（相似わかってれば十分だけど知ってると楽）
相似
平行線と面積
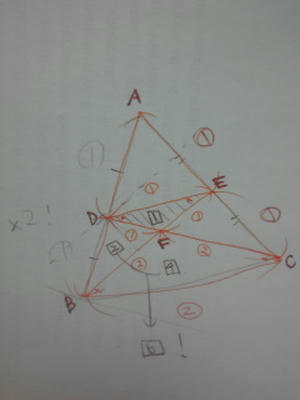
☆まず図のDF:FCの求め方。
AD:DB＝AE:EC＝1:1(DとEはそれぞれABとACの中点)
よってDE平行BC
平行線の錯角なので∠EDF＝∠FCB、∠DEF＝∠FBC
対応する二つの角がそれぞれ等しいので三角形DEF∽三角形CBF
中点連結定理（∠Aは共通、平行線の同位角なので∠ADE＝∠ABCで、二つの角がそれぞれ等しいので三角形ADE∽ABC）
三角形ADE:ABC＝1:2なのでDE:BC＝1:2
前半で証明したように三角形DEF∽三角形CBFなので
DF:FC＝1:2
☆三角形DEF:DFB
さっき証明した三角形DEF∽三角形CBFからEF:FB＝1:2
三角形DEFとDFBはBEを1:2に分けていて、高さが同じなので、面積も1:2
☆三角形DEF:DBC
三角形DBCを三角形DBFとCBFにわけて考えると三角形DBF:CBFはさっきと同じ考え方で面積比が1:2
三角形DEFを1として考えるとDBFが2でCBFがその倍の4
三角形DEF:DBC＝三角形DEF:(DBF+CBF)＝1:(2+4）＝1:6
こうだっ！
あースッキリした(笑)
[0回]
PR
